Przejdź do treści

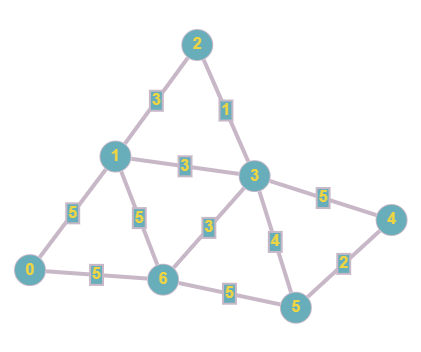
Prim

🔗 Opis problemu

Implementacja

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
#include <iostream>
#include <vector>
#include <queue>
#include <climits>

using namespace std;

struct edge {
    int from;
    int to;
    int distance;

    edge(int from, int to, int distance) {
        this->from = from;
        this->to = to;
        this->distance = distance;
    }

    bool operator<(const edge &rhs) const {
        return distance > rhs.distance;
    }
};

void prim(vector<vector<edge> > &graph, vector<edge> &minSpanningTree, int node) {
    priority_queue<edge> edges;

    vector<bool> visited = vector<bool>(graph.size());
    visited[node] = true;

    minSpanningTree = vector<edge>();

    for (int i = 0; i < graph[node].size(); i++) {
        edges.push(graph[node][i]);
    }

    while (!edges.empty()) {
        edge current = edges.top();
        edges.pop();

        if (visited[current.to]) {
            continue;
        }

        visited[current.to] = true;
        minSpanningTree.push_back(current);

        for (int i = 0; i < graph[current.to].size(); i++) {
            edge next = graph[current.to][i];
            if (!visited[next.to]) {
                edges.push(next);
            }
        }
    }
}

int main() {
    vector<vector<edge> > graph = {
        {edge(0, 1, 5), edge(0, 6, 5)}, 
        {edge(1, 0, 5), edge(1, 6, 5), edge(1, 3, 3), edge(1, 2, 3)},
        {edge(2, 1, 3), edge(2, 3, 1)},
        {edge(3, 2, 1), edge(3, 1, 3), edge(3, 6, 3), edge(3, 4, 5), edge(3, 5, 4)},
        {edge(4, 3, 5), edge(4, 5, 2)},
        {edge(5, 4, 2), edge(5, 3, 4), edge(5, 6, 5)},
        {edge(6, 0, 5), edge(6, 1, 5), edge(6, 3, 3), edge(6, 5, 5)},
    };

    vector<edge> minSpanningTree;

    prim(graph, minSpanningTree, 0);

    for(edge current : minSpanningTree) {
        cout << current.from << " <-(" << current.distance << ")-> " << current.to << endl;
    }

    return 0;
}

Opis implementacji

Na początku definiujemy strukturę edge do reprezentacji krawędzi grafu (linia 8). Ponieważ mamy do czynienia z grafem ważonym, w strukturze przechowujemy trzy wartości:

  • wierzchołek początkowy krawędzi - zmienna from (linia 9),
  • wierzchołek docelowy krawędzi - zmienna to (linia 10),
  • waga/długość krawędzi - zmienna distance (linia 11)

Dla ułatwienia definiujemy także konstruktor dla naszej struktury (linia 13). Ponieważ krawędzie chcemy przechowywać w kolejce priorytetowej, musimy także zdefiniować operator< do porównywania krawędzi (linia 19). Warto tutaj zwrócić uwagę na to, że kolejka priorytetowa z stl jest typu max, co oznacza, że domyślnie zwracałaby nam krawędź o największej wadze. Ponieważ do algorytmu Prima potrzebujemy pobierać krawędzie o najmniejszej wadze najpierw, odwracamy porządek krawędzi podczas porównywania ich wagi (linia 20).

Przykładowy graf wykorzystany w implementacji

http://graphonline.ru/en/?graph=DZlFqSBPNgdHwNXK