Przejdź do treści

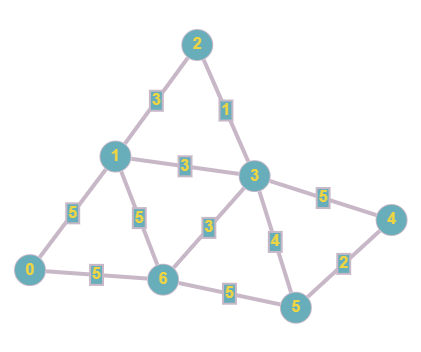
Kruskal

🔗 Opis problemu

Implementacja

  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
#include <iostream>
#include <vector>
#include <queue>

using namespace std;

class DisjointUnion {

    struct Element {
        int parent, rank;

        Element(int parent, int rank) {
            this->parent = parent;
            this->rank = rank;
        }
    };

    vector<Element> subsets;

public:

    DisjointUnion(int num_of_elements) {
        for (int i = 0; i < num_of_elements; i++) {
            subsets.push_back(Element(i, 0));
        }
    }

    int find(int x) {
        if (this->subsets[x].parent != x) {
            this->subsets[x].parent = find(this->subsets[x].parent);
        }

        return this->subsets[x].parent;
    }

    void unionn(int x, int y) {
        int x_root = find(x);
        int y_root = find(y);

        if (x_root == y_root) {
            return;
        }

        if (this->subsets[x_root].rank < this->subsets[y_root].rank) {
            this->subsets[x_root].parent = y_root;
        } else if (this->subsets[x_root].rank > this->subsets[y_root].rank) {
            this->subsets[y_root].parent = x_root;
        } else {
            this->subsets[y_root].parent = x_root;
            this->subsets[x_root].rank += 1;
        }
    }

    bool is_same(int x, int y) {
        return find(x) == find(y);
    }
};

struct edge {
    int from;
    int to;
    int distance;

    edge(int from, int to, int distance) {
        this->from = from;
        this->to = to;
        this->distance = distance;
    }

    bool operator<(const edge &rhs) const {
        return distance > rhs.distance;
    }
};

void kruskal(vector<vector<edge> > &graph, vector<edge> &minSpanningTree) {
    priority_queue<edge> edges;
    DisjointUnion connectedNodes(graph.size());

    minSpanningTree = vector<edge>();

    for(int node = 0; node < graph.size(); node++) {
        for (int i = 0; i < graph[node].size(); i++) {
            edges.push(graph[node][i]);
        }
    }

    while (!edges.empty()) {
        edge current = edges.top();
        edges.pop();

        if (connectedNodes.is_same(current.from, current.to)) {
            continue;
        }

        connectedNodes.unionn(current.from, current.to);
        minSpanningTree.push_back(current);
    }
}

int main() {
    vector<vector<edge> > graph = {
        {edge(0, 1, 5), edge(0, 6, 5)}, 
        {edge(1, 0, 5), edge(1, 6, 5), edge(1, 3, 3), edge(1, 2, 3)},
        {edge(2, 1, 3), edge(2, 3, 1)},
        {edge(3, 2, 1), edge(3, 1, 3), edge(3, 6, 3), edge(3, 4, 5), edge(3, 5, 4)},
        {edge(4, 3, 5), edge(4, 5, 2)},
        {edge(5, 4, 2), edge(5, 3, 4), edge(5, 6, 5)},
        {edge(6, 0, 5), edge(6, 1, 5), edge(6, 3, 3), edge(6, 5, 5)},
    };

    vector<edge> minSpanningTree;

    kruskal(graph, minSpanningTree);

    for(edge current : minSpanningTree) {
        cout << current.from << " <-(" << current.distance << ")-> " << current.to << endl;
    }

    return 0;
}

Opis implementacji

Definiujemy strukturę edge do reprezentacji krawędzi grafu (linia 59). Ponieważ mamy do czynienia z grafem ważonym, w strukturze przechowujemy trzy wartości:

  • wierzchołek początkowy krawędzi - zmienna from (linia 60),
  • wierzchołek docelowy krawędzi - zmienna to (linia 61),
  • waga/długość krawędzi - zmienna distance (linia 62)

Dla ułatwienia definiujemy także konstruktor dla naszej struktury (linia 64). Ponieważ krawędzie chcemy przechowywać w kolejce priorytetowej, musimy także zdefiniować operator< do porównywania krawędzi (linia 70). Warto tutaj zwrócić uwagę na to, że kolejka priorytetowa z stl jest typu max, co oznacza, że domyślnie zwracałaby nam krawędź o największej wadze. Ponieważ do algorytmu Prima potrzebujemy pobierać krawędzie o najmniejszej wadze najpierw, odwracamy porządek krawędzi podczas porównywania ich wagi (linia 71).

Przykładowy graf wykorzystany w implementacji

http://graphonline.ru/en/?graph=DZlFqSBPNgdHwNXK