Sortowanie przez wstawianie¶
Siedzisz przy stole, karty już rozdane. Spoglądasz na karty trzymane w ręce i stwierdzasz, że jak ich nie ułożysz w sensownej kolejności to się nie połapiesz. Zaczynasz więc od drugiej karty i przesuwasz ją w lewo, by trafiła na swoje miejsce. Teraz bierzesz trzecią i ponownie przesuwasz ją w lewo, aż będzie poprawnie ułożona. Podobnie postępujesz z czwartą i kolejnymi kartami: każdą kolejną bierzesz do ręki i przesuwasz w lewo, aż wstawisz ją na właściwe miejsce na ręce. Tym o to sposobem zrealizowałeś algorytm sortowania przez wstawianie.
Poniżej znajdziesz animacje przedstawiające ideę omawianego algorytmu.
Animacja 1¶
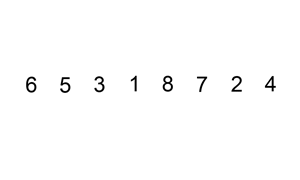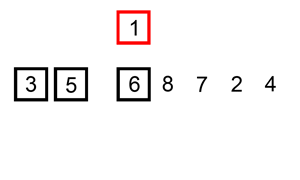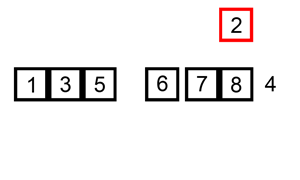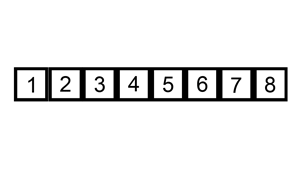
Animacja 2¶
Taneczne sortowanie¶
Rozwiązanie¶
Zaczynamy od drugiego elementu tablicy. Będziemy go przesuwać w lewo tak długo, aż nie trafi na swoje miejsce. Innymi słowy będziemy przesuwać go w lewo, dopóki nie trafi na początek tablicy i dopóki element po jego lewej stronie będzie większy. I tak postępujemy z każdym kolejnym elementem tablicy.
Pseudokod¶
procedura SortowaniePrzezWstawianie(n, A):
1. Od i := 2 do n, wykonuj:
2. j := i
3. Dopóki j > 1 oraz A[j] < A[j - 1], to:
4. Zamień(A[j], A[j - 1])
5. j := j - 1
Schemat blokowy¶
%%{init: {"flowchart": {"curve": "linear"}, "theme": "neutral"} }%%
flowchart TD
START(["SortowaniePrzezWstawianie(n, A)"]) --> K0[i := 2]
K0 --> K1{i <= n}
K1 -- PRAWDA --> K2[j := i]
K2 --> K3{"j > 1
oraz
A[j] < A[j - 1]"}
K3 -- PRAWDA --> K4["Zamień(A[j], A[j - 1])
j := j - 1"]
K4 --> K3
K3 -- FAŁSZ --> K1i[i := i + 1]
K1i --> K1
K1 -- FAŁSZ ----> STOP([STOP])Złożoność¶
\(O(n^2)\) — kwadratowa
Dwie zagnieżdżone pętle. Chociaż warunkowa pętla wewnętrzna wykonuje zawsze co najwyżej tyle obrotów, ile wynosi indeks obecnie przesuwanego elementu, to i tak otrzymujemy złożoność kwadratową, co można dość łatwo samodzielnie policzyć.