Całkowanie numeryczne¶
Hasło "całkowanie numeryczne" może brzmieć strasznie, ale samo pojęcie jest dość proste do zrozumienia. To nic innego, niż policzenie pola pod wykresem funkcji w zadanym przedziale. Oczywiście w ogólności to zadanie jest dość skomplikowane obliczeniowo, dlatego tutaj skupimy się na przybliżeniu tej wartości.
Wyróżniamy dwie podstawowe metody: metodę prostokątów i metodę trapezów.
Specification¶
Input¶
- \(f(x)\) — funkcja, której wykres nas interesuje
- \(a\) — liczba rzeczywista, początek przedziału
- \(b\) — liczba rzeczywista, koniec przedziału
- \(n\) — liczba podziałów (im większa, tym większa dokładność)
Output¶
- \(pole\) — przybliżona wartość pola pod wykresem funkcji \(f(x)\) w przedziale \([a,b]\)
Solution — metoda prostokątów¶
Idea tej metody jest prosta: podzielmy pole pod wykresem funkcji na prostokąty i policzmy ich pole.
Wizualizacja¶
Zobaczmy, jak ta metoda działa na przykładzie. Spróbujmy oszacować pole pod wykresem funkcji sinus na przedziale od \(0\) do \(\pi\).
20 prostokątów¶
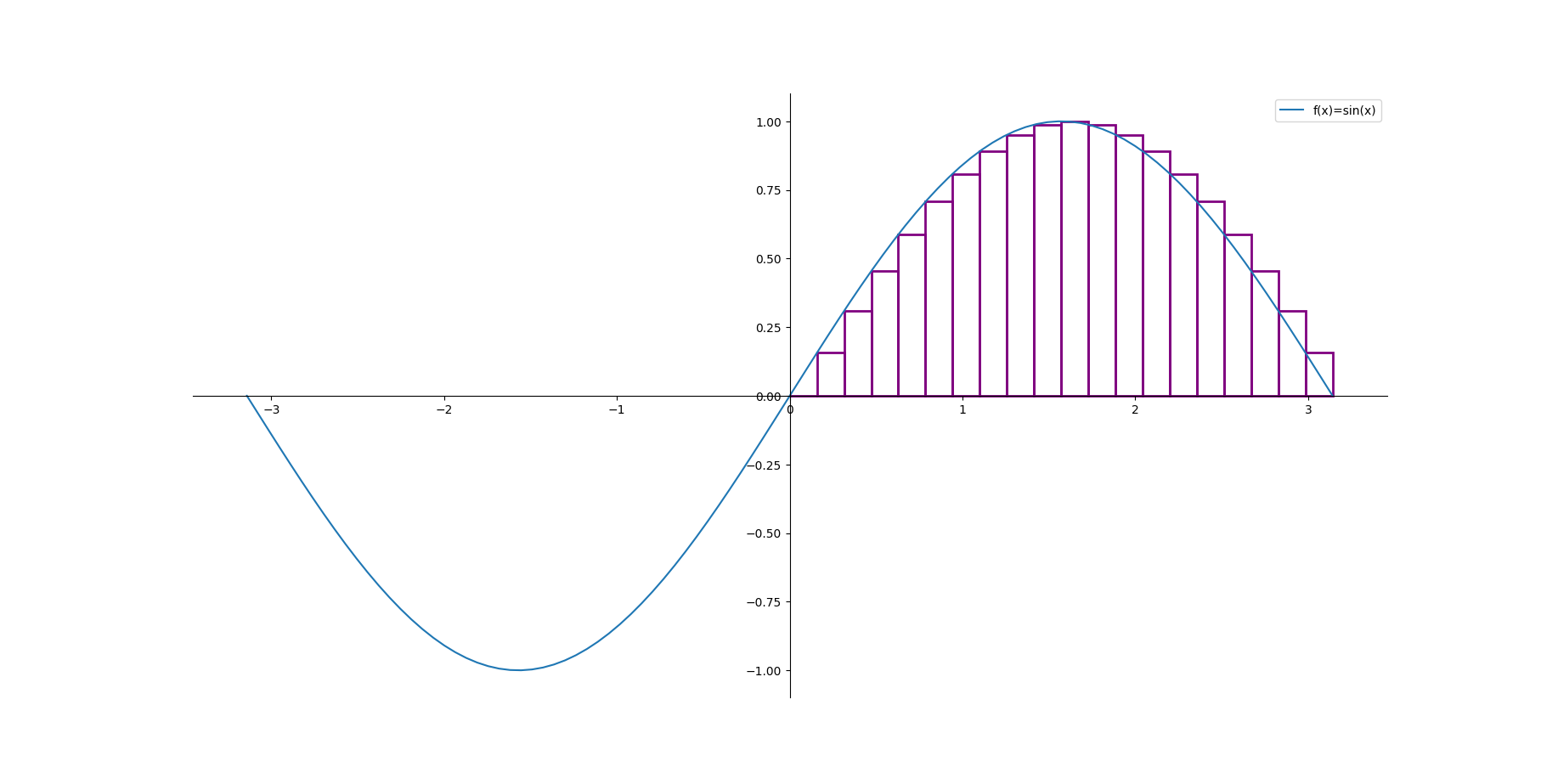
50 prostokątów¶
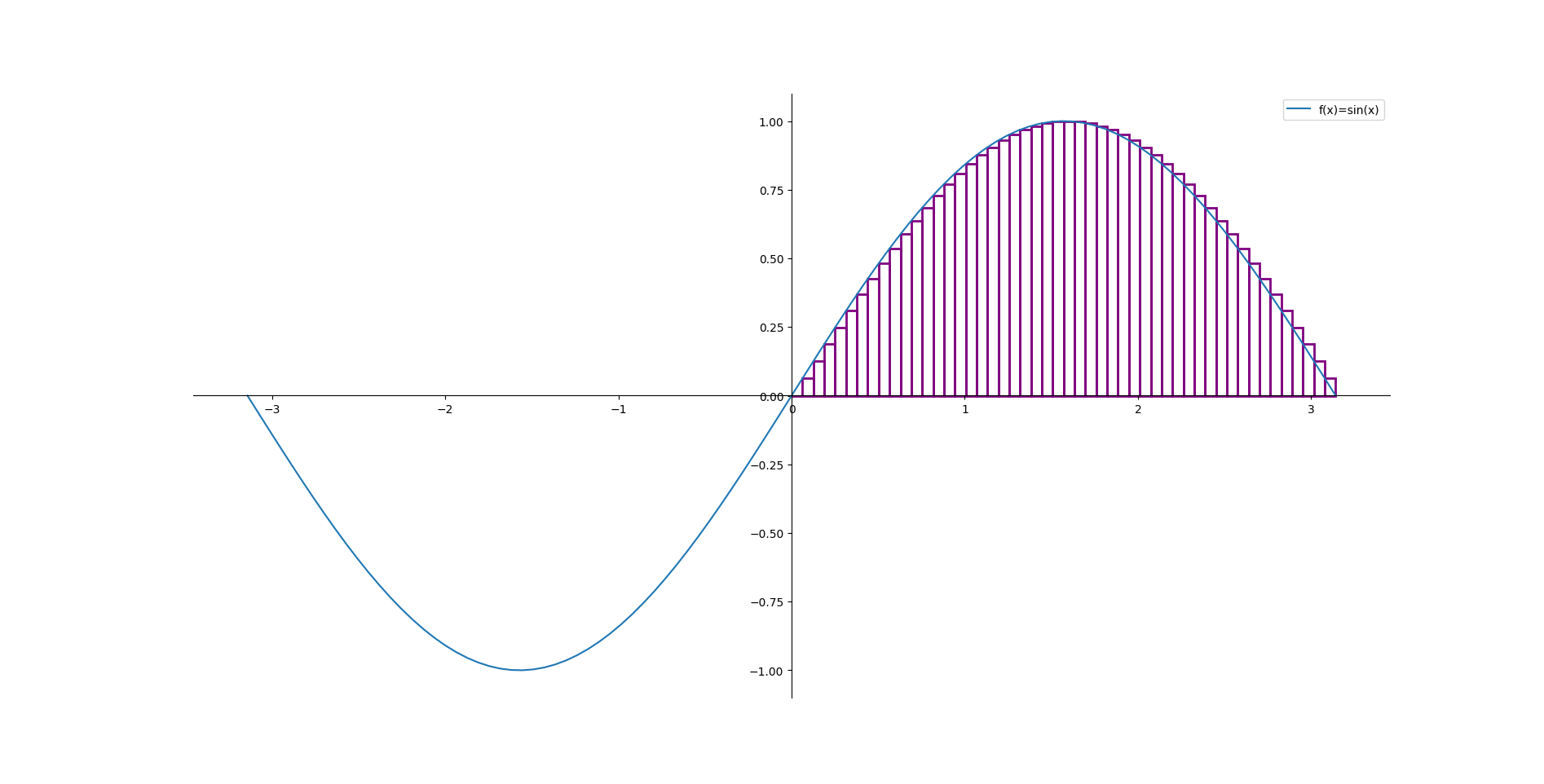
100 prostokątów¶
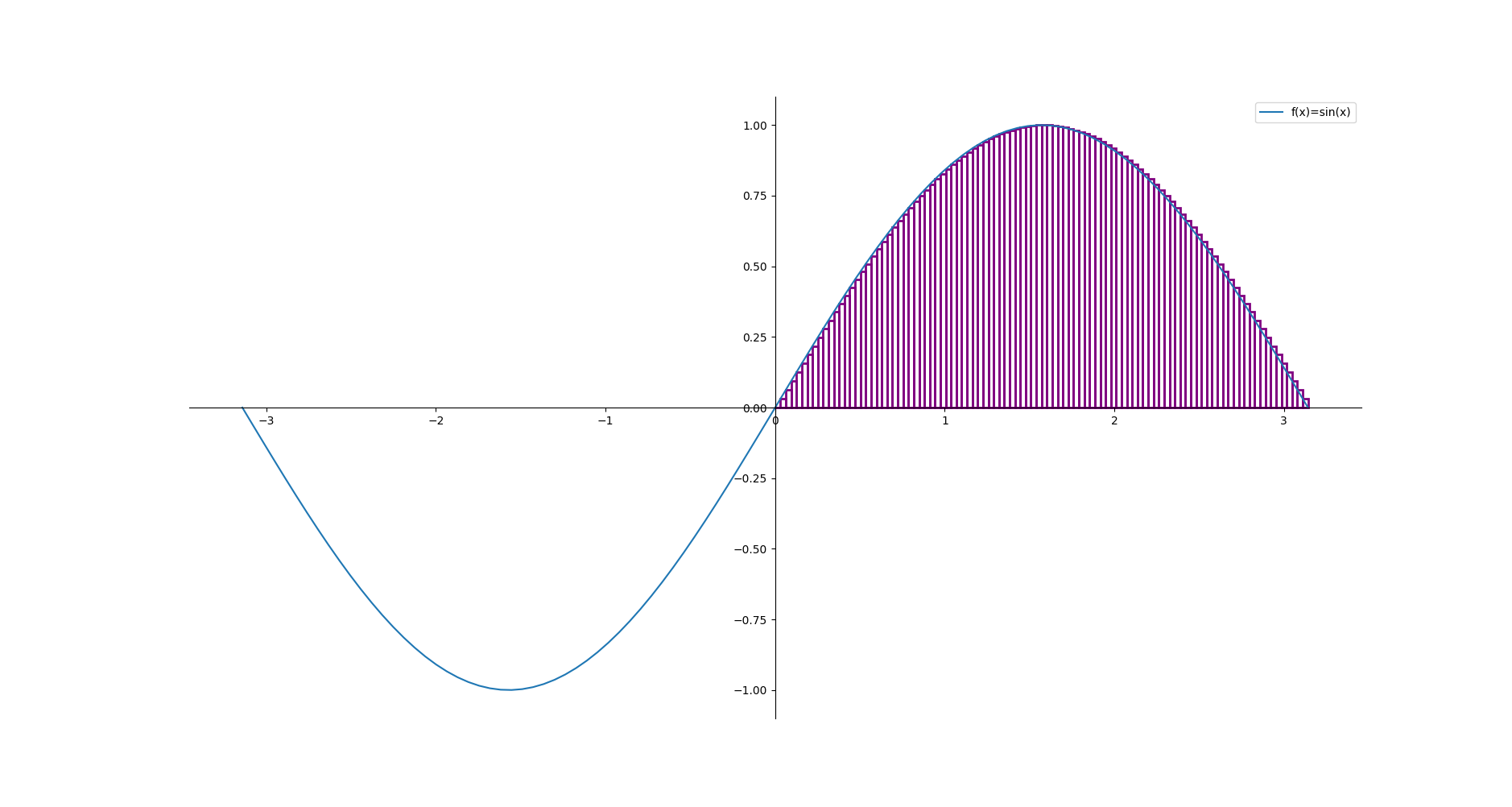
Pseudocode¶
funkcja MetodaProstokatow(f, a, b, n):
1. pole := 0
2. szer := (b - a) / n
3. x := a + szer
4. Dopóki x <= b, wykonuj:
5. wys := f(x)
6. pole := pole + szer * wys
7. x := x + szer
8. Zwróć pole
Block diagram¶
%%{init: {"flowchart": {"curve": "linear"}, "theme": "neutral"} }%%
flowchart TD
START(["MetodaProstokatow(f, a, b, n)"]) --> K1["pole := 0
szer := (b - a) / n
x := a + szer"]
K1 --> K4{x <= b}
K4 -- TRUE --> K5["wys := f(x)
pole := pole + szer * wys
x := x + szer"]
K5 --> K4
K4 -- FALSE --> K8[/Zwróć pole/]
K8 --> STOP([STOP])Solution — metoda trapezów¶
W celu uzyskania lepszej dokładności, możemy podzielić pole pod wykresem funkcji na trapezy.
Pseudocode¶
funkcja MetodaTrapezow(f, a, b, n):
1. pole := 0
2. szer := (b - a) / n
3. x := a + szer
4. Dopóki x <= b, wykonuj:
5. pole := pole + ((f(x - szer) + f(x)) * szer) / 2
6. x := x + szer
7. Zwróć pole
Block diagram¶
%%{init: {"flowchart": {"curve": "linear"}, "theme": "neutral"} }%%
flowchart TD
START(["MetodaTrapezow(f, a, b, n)"]) --> K1["pole := 0
szer := (b - a) / n
x := a + szer"]
K1 --> K4{x <= b}
K4 -- TRUE --> K5["pole := pole + ((f(x - szer) + f(x)) * szer) / 2
x := x + szer"]
K5 --> K4
K4 -- FALSE --> K8[/Zwróć pole/]
K8 --> STOP([STOP])